¿Cómo usarlo?

Conceptos Teóricos

El Teorema de Pitágoras se aplica exclusivamente a triángulos rectángulos y no es mas que una relación entre todos sus lados; dentro de los tipos de triángulos se clasifican como rectángulos a aquellos que poseen un ángulo recto es decir un ángulo de 90°, por tanto los triángulos Acutángulos (con todos sus ángulos agudos, es decir,  inferiores a 90°) y los Obsutángulos (con al menos un ángulo obtuso, es decir, mayor que 90°) no pueden resolverse a través de este teorema directamente y necesitan de otras herramientas matemáticas como los teoremas del Seno y Coseno.

Los lados mas cortos de un triángulo rectángulo son conocidos como catetos y el mas largo es llamado hipotenusa, tambien podemos definirla como el lado opuesto al ángulo recto, es decir, el lado al otro extremo del ángulo de 90°. Todos los triángulos rectángulos por definición tienen dos catetos y la hipotenusa, y el Teorema de Pitágoras se encarga de relacionarlos permitiendo encontrar algunas de esas tres variables cuando se conozcan dos de ellas.

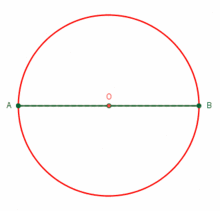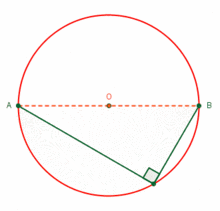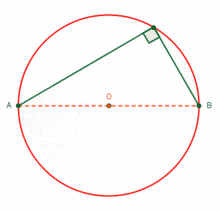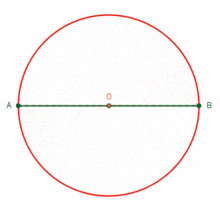
Figura 2.2.: Distintas presentaciones de un Triángulo Rectángulo

 

Figura 2.3.: Lados de un triángulo rectángulo

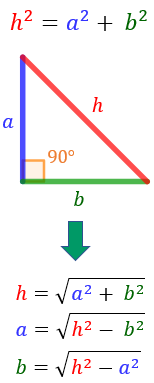
El Teorema de Pitágoras nos indica que la suma de los cuadrados de los catetos nos dará como resultado el cuadrado de la hipotenusa. En esta relación mostrada en la ecuación de la Figura 2.4 la hipotenusa es representada por la letra 'h' y los catetos con las letras 'a' y 'b', estos últimos pueden seleccionarse de cualquier manera ya que la propiedad conmutativa de la suma permite que el resultado no se afecte si una persona toma un cateto como el 'a' y el otro como el 'b' y otra persona los escoje de manera contraria, en ambos casos el resultado no se verá afectado.

Figura 2.4.: Teorema de Pitágoras

Ejemplo 1

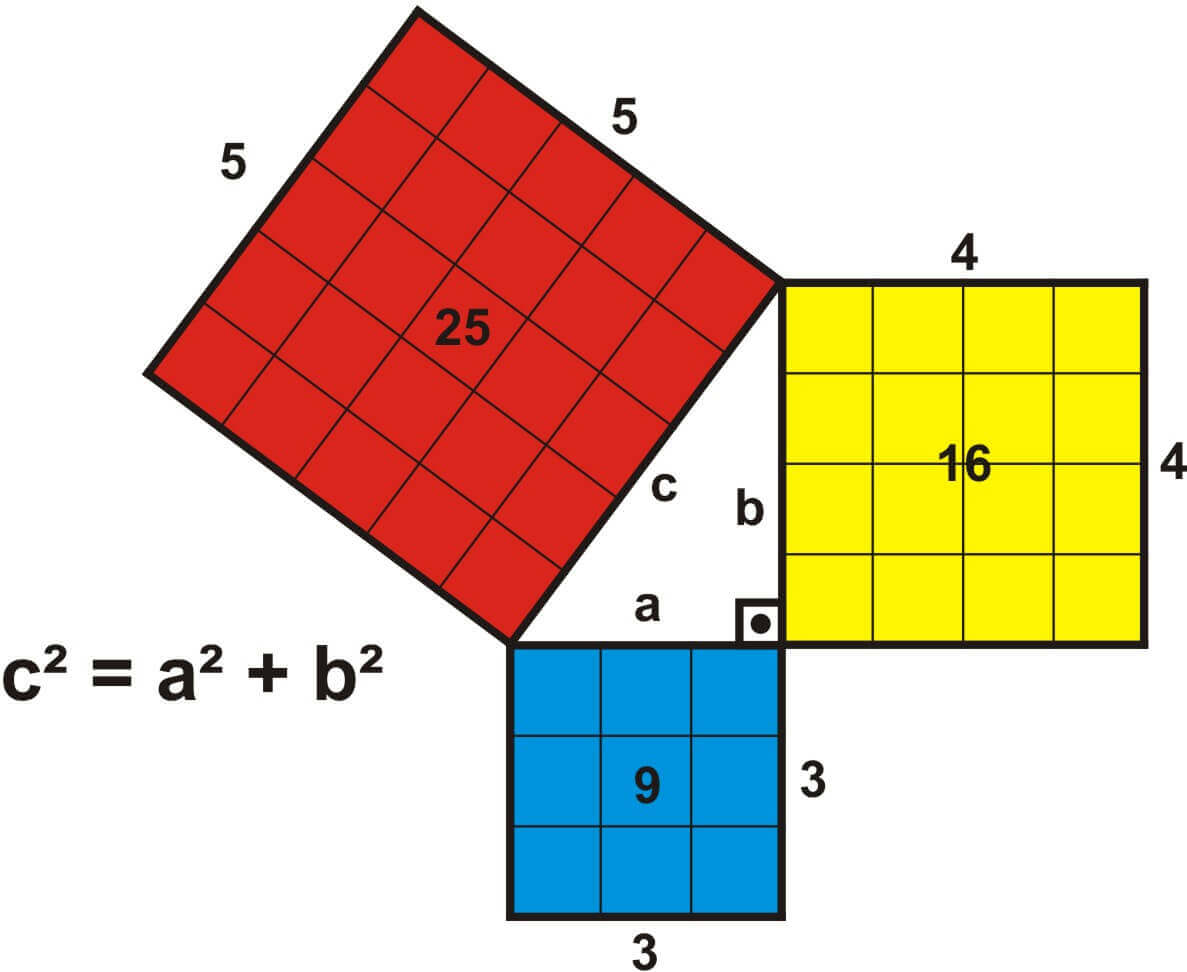
Una representación clásica de este teorema es el presentado en la Figura 2.5, aquí podemos observar de manera intuitiva cómo se cumple el teorema de pitágoras, al tratarse de cuadrados, observamos que el azul tiene lados con una distancia de tres unidades, así mismo se observa que los lados del cuadrado amarillo son de cuatro unidades y que al organizarlos de la manera mostrada se necesitaría un cuadrado (como el rojo) de cinco unidades de lado para que en el espacio encerrado se forme un triángulo rectángulo. En este ejemplo se observa que la relación entre los catetos a y b de tres y cuatro unidades respectivamente con su hipotenusa de cinco unidades se aprecia en el cuadrado de estos valores ya que la suma de las nueves unidades cuadradas mas las dieciseis unidades cuadradas de los cuadrados que forman los catetos son iguales a las veinticinco unidades cuadradas que forman el cuadrado rojo cuyo lado es la hipotenusa, de ahí la formula del Teorema de Pitágoras.

Figura 2.5.: Demostración geométrica del Teorema de Pitágoras

"Nótese que en el caso anterior se reemplazó la letra 'h' de la hipotenusa por una 'c', esto es sólo un cambio de nomenclatura que no afecta el desarrollo o solución de cualquier ejercicio, sin embargo es importante tener claro a que se refiere cada concepto para que no se presenten errores cuando encontramos las fórmulas de manera distintas a cómo las conocimos inicialmente."

Ejemplo 2


Volvamos a la Figura 2.4 y suponemos que el cateto 'a' es igual a seis unidades y el cateto 'b' es igual a ocho unidades, hallaremos la hipotenusa mediante el Teorema de Pitágoras. 

Procedemos a escribir la fórmula del Teorema de Pitágoras:

 h² = a² + b²

A continuación reemplazamos los valores conocidos, en este caso sabemos que a=6 y b=8, por tanto:

 h² = 6² + 8²

 Calculamos los cuadrados de los catetos (6²=36 y 8²=64), y procedemos a sumarlos tál cómo lo indica la fórmula:

 h² = 36 + 64

 h² = 100 

Por último aplicamos raíz cuadrada a cada lado de la igualdad obteniendo el valor de la hipotenusa:

  √ (h²) =  √ (100) 

h = 10

Concluimos entonces que la hipotenusa tiene una valor de 10 unidades.



Ejemplo 3

En algunos casos es uno de los catetos el que desconocemos, por lo tanto para este ejemplo asumiremos conocidos los valores de la hipotenusa (h= 9 unidades) y uno de los catetos (b= 4 unidades) y procedemos a calcular el cateto faltante (a) utilizando el Teorema de Pitágoras:

 h² = a² + b²

Como esta vez debemos hallar el cateto 'a', procedemos a despejarla de la ecuación, para ello debemos anular el término 'b²' que se encuentra sumando a su lado, procedemos entonces a restar ese término en ambos lados de la igualdad así:

 h² - b² = a² + b² - b²
 h² - b² = a² + b² - b²
h² - b² = a² + 0
h² - b² = a²

Reordenamos la ecucación sin cambiar sus signos para que tengan una forma típica de las ecuaciones matemáticas:

a² = h² - b² 

Reemplazamos los valores conocidos (h=9 y b=4) y procedemos a calcular como en el ejemplo 2, debemos tener en cuenta que luego de resolver las potencias cuadradas debemos realizar una resta y no una suma como ocurrió en el caso anterior:

a² = h² - b² 

a² = 9² - 4² 

a² = 81 - 16

a² = 65

√(a²) = √(65)
a = 8,06... 

Con lo cual podemos afirmar que el cateto desconocido tiene un tamaño de aproximadamente 8 unidades.

 "Algunas personas asumen la ecuación para hallar catetos como una fórmula distinta, sin embargo es la misma relación presentada en el Teorema de Pitágoras, sólo que despejada según las condiciones del ejercicio. Es importante saber cuando utilizarla ya que es uno de los errores típicos que se cometen en el estudio de esta temática"


 


Ejemplo 4

Observemos la situación que se presenta a continuación:

Podemos observar una situación que requiere del uso del teorema de Pitágoras, cuyo valor desconocido es la hipotenusa (nótese que se refieren a que necesitan hallar la diagonal). En la tira cómica se aprecia un cálculo rápido para hallar tal incognita, por tanto realizamos su comprobación y validamos el resultado allí presentado:

 h² = a² + b²

 h² = (100cm)² + (60cm)²

 h² = 10000cm² + 3600cm²

 h² = 1360cm²

√ (h²) = √(13600cm²) 
h= 116,61... cm

Podemos afirmar entonces que el cálculo de la hipotenusa estuvo bien realizado.

Como se ha podido observar el teorema de Pitágoras puede llegar a ser realmente útil y es aplicable a distintas situaciones incluso de manera cotidiana en la vida, por ello su dominio se ha convertido en parte de la cultura general, para finalizar sólo les recomendamos que realicen abundantes ejercicios ya que la práctica es la mejor manera de comprender a cabalidad cualquier nuevo reto que las matemáticas nos pongan al frente.